
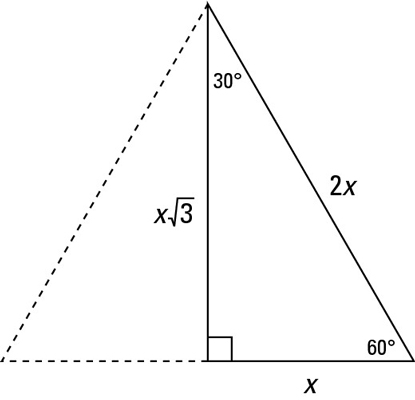
Now that we've proven the congruencies of the two new triangles, we can see that the top angles must each be equal to 30 degrees (because each triangle already has angles of 90° and 60° and must add up to 180°). Basically? They're most definitely congruent. Note: not only are the two triangles congruent based on the principles of side-side-side lengths, or SSS, but also based on side-angle-side measures (SAS), angle-angle-side (AAS), and angle-side-angle (ASA). Because they share three side lengths in common (SSS), this means the triangles are congruent. The new triangles also share one side length (the height), and they each have the same hypotenuse length. How do we know they're equal triangles? Because we dropped a height from an equilateral triangle, we've split the base exactly in half. We've now created two right angles and two congruent (equal) triangles. Now let's drop down a height from the topmost angle to the base of the triangle. Because a triangle's interior angles always add up to 180° and $180/3 = 60$, an equilateral triangle will always have three 60° angles. Why It Works: 30-60-90 Triangle Theorem Proofīut why does this special triangle work the way it does? How do we know these rules are legit? Let's walk through exactly how the 30-60-90 triangle theorem works and prove why these side lengths will always be consistent.įirst, let's forget about right triangles for a second and look at an equilateral triangle.Īn equilateral triangle is a triangle that has all equal sides and all equal angles. No need to consult the magic eight ball-these rules always work. Because this is a 30-60-90 triangle and the hypotenuse is 30, the shortest leg will equal 15 and the longer leg will equal 15√3. So long as you know the value of two angle measures and one side length (doesn't matter which side), you know everything you need to know about your triangle.įor example, we can use the 30-60-90 triangle formula to fill in all the remaining information blanks of the triangles below.Īgain, we are given two angle measurements (90° and 60°), so the third measure will be 30°. Though it may look similar to other types of right triangles, the reason a 30-60-90 triangle is so special is that you only need three pieces of information in order to find every other measurement.

And, finally, the side opposite the 90° angle will always be the largest side (the hypotenuse) because 90 degrees is the largest angle. The side opposite the 60° angle will be the middle length, because 60 degrees is the mid-sized degree angle in this triangle. The side opposite the 30° angle is always the smallest, because 30 degrees is the smallest angle. And the hypotenuse is 2 times the shortest leg, or $2√3$) (Why is the longer leg 3? In this triangle, the shortest leg ($x$) is $√3$, so for the longer leg, $x√3 = √3 * √3 = √9 = 3$. Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another.įor example, a 30-60-90 degree triangle could have side lengths of: So let's get to it!Ī 30-60-90 triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees.
In this guide, we'll walk you through what a 30-60-90 triangle is, why it works, and when (and how) to use your knowledge of it. And a 30-60-90 triangle-pronounced "thirty sixty ninety"-happens to be a very special type of triangle indeed. Acute, obtuse, isosceles, equilateral…When it comes to triangles, there are many different varieties, but only a choice few that are "special." These special triangles have sides and angles which are consistent and predictable and can be used to shortcut your way through your geometry or trigonometry problems.


 0 kommentar(er)
0 kommentar(er)
